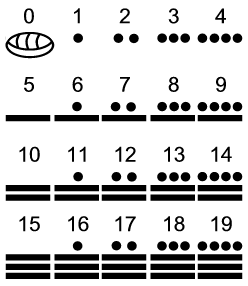
Цифры майя

Матема́тика ма́йя в своей основе использовала двадцатеричную систему счисления для записи чисел . Вычисления производились на специальном приспособлении (наподобие абака ), счётными единицами которых служили какао-бобы или различные по цвету камешки. Математика позволяла майя производить сложные подсчёты в хозяйственной деятельности , была базой многих точных наук , которые оперировали числами. Уровень развития математики майя, учитывая сложность некоторых вычислений, найденных в виде записей на некоторых плитах (например, стела № 10 в Тикале ), опережал развитие математических знаний Старого Света .

Цифры майя

Система счёта майя представлена двадцатеричной позиционной системой счисления . То есть в отличие от индийской десятеричной системы конец первого разряда приходился на число 20 , но, как и в ней, числа имели свой разряд : единицы, двадцатки, четырёхсотки и так далее (каждый новый разряд умножает значение предыдущего в двадцать раз).

Запись числа производилась всего лишь при помощи трёх элементов: единица — точка, пять — черта, нуль — раковина. Наличие нуля в счёте майя является неоспоримым свидетельством того, что развитие математики у изолированного от остального света вплоть до XVI века народа стояло на высоком уровне. Неизвестно, когда именно был введён нуль. Первое свидетельство его использования было найдено на стеле № 2 в Чиапасе и датируется 36 годом нашей эры .

Запись происходила вертикально, причём первый разряд находился внизу, второй — выше первого, третий — выше второго и далее. В нижней части числа заканчивались на 19-ти , и далее над ним (как обозначение перехода на следующий разряд) ставилась точка, обозначающая единицу. Собственно число двадцать можно было представить как раковина (нуль) и точка (двадцать) над ней. Числа, больше 400 записывались, соответственно, в три ряда. Так, число 431 выглядело как две черты с точкой ( 11 ) одна точка на второй линейке (20) и одна точка на третьей ( 400 ). Таким образом, 11 + 20 × 1 + 400 × 1 = 431 .

Математика майя в историографии

Во многих источниках отношение к развитию математики у майя описано как «удивительно противоречивое явление» . С одной стороны, майя отставали от европейцев на многие годы, а с другой — смогли создать систему счёта, опережающую европейскую. В частности, Диего де Ланда отмечал необычайный уровень развития абстрактного мышления у индейцев , мотивируя это тем, что они были способны оперировать колоссальными числами:

Их счёт ведётся по 5 до 20, по 20 до 100, по 100 до 400 и по 400 до 8000… У них есть другой счёт, более длинный, который они продолжают до бесконечности, считая 8 тысяч 20 раз, что составляет 160 тысяч, затем, возвращаясь к 20, они умножают 160 тысяч на это число и так продолжают умножать на 20, пока не получат громадной цифры. Они считают на земле или на чём-нибудь гладком .